Triángulos
Pruebas de selección para Estalmat 2010
Se tiene un cuadrilátero convexo (con todos sus ángulos menores de 180 grados), como el de la primera imagen, y sobre cada uno de sus lados y en el exterior de ese cuadrilátero se dibujan triángulos equiláteros.
a) ¿Cuánto vale la suma de todos los ángulos que se forman entre triángulos equiláteros contiguos?
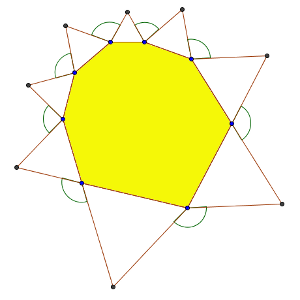
Ahora, en vez de un cuadrilátero, tenemos un polígono de ocho lados convexo, y también dibujamos triángulos equiláteros sobre sus lados en el exterior de ese polígono. Hemos representado un polígono de ese tipo en el segundo dibujo.
b) ¿Cuánto vale la suma de todos los ángulos que se forman entre triángulos equiláteros contiguos?
Por último, imagina que dibujas un polígono de 1000 lados, que sea también convexo, y sobre cada lado un triángulo equilátero hacia fuera.
c) ¿Cuánto valdría la suma de todos los ángulos que formaran los triángulos equiláteros contiguos?




2 comentarios:
Partimos de la base de que la suma de ángulos exteriores de un polígono solo depende del numero de lados.
Empezamos por el menor, tenemos 4 ángulos que llamaremos A,B,C,D, al insertar los triángulos equiláteros en los lados, el ángulo será igual al complementario menos 60º por triángulo:
A=A => A’=360-120-A y sucesivamente por lo que sabemos que el total buscado será:
A’+B’+C’+D’ = (360-120-A)+(360-120-B)+(360-120-C)+(360-120-D)
A’+B’+C’+D’ = 4•(360-120)-(A+B+C+D)
A’+B’+C’+D’ = 4•240-(A+B+C+D)
De aquí obtenemos el factor 4, equivalente al numero de lados, que podemos generalizar a n
N’ = n•240-(A+B+C+D)
Faltaría saber la suma de ángulos de un polígono de n lados.
Sabemos que la suma para n=4 es 360, n=6 es 720 y n=8 es 1080, por lo que deducimos que es igual a 180•(n-2)
N’ = n•240-(180•(n-2)) = 240n-180n+360 = 60n+360
Ahora podemos aplicar los valores conocidos para n:
f(n=4) = 60•4+360 = 240+360 = 600
f(n=8) = 60•8+360 = 480+360 = 840
f(n=1000) = 60•1000+360 = 60000+360 = 60360
Respecte a la suma dels angles interiors d'un poligon convex de n costats, que el comentari anterior suposa (correctament) en (n-2)pi
Dem: resulta senzill demostrar que la suma dels angles interiors d'un triangle és pi (un angle pla). Lamentablement no sé introduir dibuixos en els comentaris, i per tant, aquest lemma el deixarem per al lector...
Resulta òbvi que es pot partir un poligon convex en n-2 triangles (uneix un vèrtex amb tots els altres, de la definició de convexitat cap segment entre vèrtex queda fora...)
Es veu clar que la suma dels angles d'aquests triangles és igual a la suma dels angles del polígon. (es veu clar amb un dibuix)
Per tant, queda provada la suposició de David...
Publicar un comentario